重力是什麼?愛因斯坦的廣義相對論
摘自 25.05.2017余海峯 DAVID | 物理喵 PHYCAT
亞里士多德說重力是一種向下跌的慣性,物件越重下跌速度越快;牛頓說重力是物質互相吸引的萬有引力造成的,而且不論物件多重,下跌加速度都相同;愛因斯坦說,宇宙間根本沒有重「力」,物件之所以會互相吸引,是因為質量把時空扭曲了,物質沿著四維時空曲率「下跌」。
等等,我們不是活在三維空間裡面嗎?我們知道這個宇宙中有三個互相垂直的方向:前後、左右、上下。愛因斯坦發現,如果把時間也視作維度,就能用相對論描述整個宇宙的演化。三維空間加一維時間,構成了我們身處的宇宙。數學家能夠把 N 個維度的幾何規則推導出來,不過這個宇宙似乎只需要四維就足夠。
牛頓對決馬克士威
牛頓在 1687 年出版《自然哲學的數學原理》,闡述了他發現的運動定律和萬有引力定律。其實在牛頓的力學架構中,時間早己是一個維度。要討論力學,我們必須引入參考系概念。請不用擔心,參考系就是我們在基礎數學裡學過的座標而已。如果把三維空間的三個方向叫做x、y、z,而時間叫做 t 的話,那麼要在兩個參考系 S 和 S' 之間轉換,牛頓就說
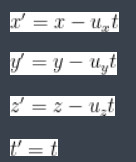
其中 Ux、Uy、Uz 分別是參考系 S' 相對參考系 S 在 x、 y、 z 方向上的速度,另外我們假設了 S 和 S' 在時間 t=0 時重合。這一組四式,我們稱之為伽利略變換。
我們可以看出,時間這個維度在牛頓力學體系裡,無論相對哪個參考系都是一樣的。換句話說,對於任何觀測者而言,彼此的時間都永遠相同。牛頓說,宇宙有一個絕對的時鐘,時間流逝速率對於任何人都一樣,永恆不變。
另一方面,因為速度等於位移除以時間,無論觀察的人跑得多快,一個物件的長度都不會改變。這就是牛頓的絕對時空觀,從 17 世紀到 19 世紀統治著物理學。在這段期間內所有科學實驗結果都與牛頓力學吻合,因此我們可說所有古典科學結論都建基於牛頓力學。
之不過,牛頓力學的天空在 19 世紀後半期已經開始烏雲密佈。如果時空的確是絕對的,那麼我們就可以找到一個絕對靜止的參考系。根據馬克士威在 1861 和 1862 年發表的電磁波動方程,電磁波——光——的速度是固定的,數值是秒速 299,792,458 米。這就引申了一個問題:光速相對哪個參考系有此定值?如果找到一個參考系,在這參考系之中測量的光速等於每秒 299,792,458 米,那麼這個就是絕對靜止的參考系。
當時的物理學家稱呼這個參考系做以太,認為以太就是光線的傳播媒介。如果宇宙是絕對靜止的,以太這個特別的參考系就好像宇宙本身,宇宙間一切事物都相對以太運動,而光速只有在以太參考系裡才是秒速 299,792,458 米。
然而,科學進程往往曲折離奇、耐人尋味。1887 年,邁克生和莫雷合作做了一個實驗,去測量地球在以太中的速度。他們用的儀器叫做干涉儀,可以精確地量度光速在兩個互相垂直的方向的差別,稱為光程差。因為地球環繞太陽運動,他們預期在四季不同日期會測量到不一樣的光程差。令所有人驚訝的是,光程差在一年中任何時間都一樣是零!
邁克生和莫雷的實驗結果顯示,無論觀測者的運動速率和方向,光速都一樣是秒速 299,792,458 米,絲毫不差。這個發現與牛頓力學完全相反,根據伽利略轉換,速度是會疊加的,所以在移動中的地球上沿不同方向行進的光線速率就是每秒 299,792,458 米加或減地球在該方向上相對以太參考系的速率。這是牛頓力學和馬克士威電磁波動方程結合的結果,可是大自然卻說這是錯的!
少年愛因斯坦的煩惱
問題到底出在哪裡呢?當時的物理學界並不知道,在德國南部城市慕尼黑裡,一個高中生的腦海裡的一個問題,竟然是答案的關鍵。愛因斯坦原本在慕尼黑讀高中,因為忍受不住德國軍訓式的課堂教育,以精神健康問題為由中途退學,到瑞士一個叫阿勞(Aarau)的小鎮完成中學課程,同時準備報考蘇黎世聯邦理工學院(ETH Zürich)。
從慕尼黑的中學到他自蘇黎世聯邦理工學院畢業、並在朋友的幫助下勉強找到一份瑞士專利局二級專利員工作的期間,這個問題一直佔據著愛因斯坦的思緒:如果一個人能夠騎在光束之上,會看見靜止的電磁波嗎?根據牛頓時空觀,答案是肯定的。可是,馬克士威的電磁理論中並沒有用到以太這個概念。如果光速恆定這結論適用於所有參考系呢?可是,這樣牛頓和馬克士威的理論就互相矛盾了。馬克士威錯了嗎?不可能,他的電磁理論太美麗了,不可能錯的⋯⋯牛頓錯了嗎?可是,兩百多年來他的理論從未出錯⋯⋯抑或是兩個都錯了?
顯然,這裡有個難題,而難題的解答並不會使牛頓和馬克士威皆大歡喜。「我們的常識哪裡出錯了嗎?」愛因斯坦問道。
愛因斯坦通常只用半天就完成整天要做的工作,然後他就會在專利局辦公桌上思考和推導物理。一天,他突然發現了我們常識中的漏洞,而這個靈感徹底改變了世界。
愛因斯坦想像有一列以超高速行駛的火車,在直線路軌兩端上的雲同時閃電。我們身處火車中央,相隔兩道閃電的距離剛好一樣。愛因斯坦問:我們會看到閃電同時發生嗎?答案是不會的,因為火車正向前面那道閃電駛過去,同時遠離後面那道閃電,因此我們會首先看見前面的閃光。現在,如果在路軌旁的地面站著我們的朋友,他亦距離兩道閃電同樣遠。因為他相對兩道閃電而言都是靜止的,他就會看見兩道閃電同時發生。
這就導致了一個驚人的結論:「同時」這個概念並非絕對,兩件事情的發生次序,與觀測者的運動狀態有關!換句話說,時間是相對的。
意識到時間並非絕對的愛因斯坦,在 1905 年發表了一篇題為《論動體的電動力學》的論文。他在論文中以不同運動狀態觀察法拉弟電磁感生效應,推導出狹義相對論的參考系變換公式:
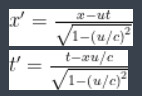
 為簡化表達式,我們設 S' 沿 x 軸方向運動。狹義相對論的所有結論都可以由這裡開始推導出來,我們稱之為洛倫茲變換。
為簡化表達式,我們設 S' 沿 x 軸方向運動。狹義相對論的所有結論都可以由這裡開始推導出來,我們稱之為洛倫茲變換。
速率 = 距離/時間。三個變數,如果其中一個不變而另一個改變,那麼第三個變數也就必須改變。常識說時間是絕對的,如果光線走過的距離改變,其速率也會改變。愛因斯坦指出時間並非絕對,光速才是。時間的改變補償了距離的改變,使光速永遠不變。
原來,我們對於時間的常識有誤;原來,馬克士威是正確的,錯的是牛頓;原來,光線能夠在真空中傳播,並不需要以太。就是這篇論文,再加上愛因斯坦同年發表的另一篇論文《一個物體的慣性依賴於它所包含的能量嗎?》推導出史上最著名的公式 E=mc² ,狹義相對論從此取代牛頓的絕對時空觀。
十年光陰追逐重力 答案就在等效原理
愛因斯坦的狹義相對論並沒有考慮重力。愛因斯坦發表狹義相對論後,就致力尋找一個更廣義、能把重力包括進去的相對時空理論。
這裡要提一個經常出現的錯誤觀念:狹義相對論不適用於加速的情況。例如,有個誤解是雙生子佯謬違反了狹義相對論,這是不正確的。狹義相對論能夠描述物件受力加速,也能夠處理加速參考系(即非慣性參考系)的情況。誤解可能來自於在狹義相對論裡,慣性和非慣性參考系的處理有所不同。但這只不過跟牛頓力學一樣,在非慣性參考系裡的觀測者會看到虛擬的力,例如離心力和科氏力等,都不是真正的力。但物理上,加速度對狹義相對論完全沒有影響。
既然如此,我們為什麼需要廣義相對論?既然狹義相對論可以處理加速度,那麼把牛頓的萬有引力定律放進去不就可以了嗎?愛因斯坦也曾嘗試這樣做,但牛頓萬有引力定律的問題在於所謂的超距作用:重力不用任何時間就能傳遞,而相對論卻說沒有資訊能夠超越光速。其實電磁力的情況也一樣,物理學家需要考慮電磁力傳遞的時間差,這是我們在大學物理課會學到的所謂推遲勢。由於電磁波就是光,電磁力的傳播速度就是光速。如果我們假設重力的傳播速度也是光速,同樣利用推遲勢把萬有引力定律改造,得出的計算數值與觀測結果並不相符。
另一方面,除了把重力包括在內,廣義相對論對慣性和非慣性參考系一視同仁。這是因為狹義相對論的時空只能是平直的,而廣義相對論的時空則可以是彎曲的。換句話說,在狹義相對論裡我們只能用「直線」來畫座標系,而在廣義相對論裡用任何曲或直的線來畫都可以。
1907 年,愛因斯坦突然靈機一觸,想到了等效原理(equivalence principle)。試想像我們身處一艘太空船裡,太空船沒有窗戶。我們發現自己感覺就如日常一樣。那麼,我們能否分辨太空船究竟正停泊在地球上,還是以與地球的地心加速度大小一樣的加速度往上加速?愛因斯坦說,我們不可能分辨得到。另外一個假想實驗是我們身處一部電梯之中,然而我們感受不到任何重力。那麼我們又能否分辨電梯究竟正在往下跌,還是漂浮在太空之中?愛因斯坦說,我們同樣不可能分辨得到。等效原理指出,重力和加速度並不單止效應相同,兩者實際上是同樣的東西!
愛因斯坦回憶說,想到了等效原理的一刻,是他一生中最快樂的一刻。然而,他往後足足用了八年時間,才能由等效原理建構出正確的廣義相對論公式。在尋找正確方程的過程中,愛因斯坦發現他知道的數學工具並不足夠。廣義相對論處理的是彎曲的時空,需要用到所謂的非歐幾里得幾何學。愛因斯坦在蘇黎世聯邦理工學院的同學格羅斯曼正好是研究非歐幾何學的教授,因此愛因斯坦向他請教了很多數學上的問題。縱使格羅斯曼並沒有直接參與廣義相對論的研究,他對愛因斯坦的幫助是找到正確方程的關鍵。
廣義相對論處理的非歐幾何時空問題,需要使用張量、度規、協變導數的數學概念。張量可想像成具有多個方向的向量,雖然數學上這不完全正確;度規用來描述時空的幾何結構,定義了在非歐幾何上距離的計算規則;協變導數則是在非歐幾何上做微分的方法。我們不用深入探討每一項,也能知道要得心應手地使用這些工具,必須經過長時間的數學訓練。雖然愛因斯坦的數學不差,他始終不是專業的數學家。
1915 年暑假,愛因斯坦受數學家希爾伯特邀請到哥廷根科學院(Akademie der Wissenschaften zu Göttingen)講了六場講座。他們互相交流了意見,而希爾伯特也開始尋找正確的廣義相對論公式。希爾伯特的進展非常快,漸漸令愛因斯坦感受到很大壓力,他害怕希爾伯特會比自己先找到正確公式。愛因斯坦在同年 11 月於柏林普魯士科學院(Preußische Akademie der Wissenschaften)講了四場講座,並在最後一場發表了他發現的廣義相對論方程式:

![]()
現在,我們稱之為愛因斯坦場方程式(Einstein field equations)。這是一組十式獨立的張量微分方程組(對,一條公式已包含了十條方程),方程組的解不單止能夠描述物體在重力影響下的運動,更能描述整個宇宙的演化。因為在廣義相對論裡,時空就是宇宙本身。
驗證廣義相對論
廣義相對論說,物體並非受引力吸引,而是沿著四維時空的曲率「下跌」。而扭曲時空的,就是質量。相對論大師惠勒曾用一句精闢的話總結愛因斯坦場方程式:
「時空告訴物質如何運動,物質告訴時空如何彎曲。」
以下這個比喻是標準的廣義相對論解釋:想像有張彈床,彈床上放了個保齡球,令彈床向下陷。一個乒乓球滾過保齡球旁邊,就向彈床下陷的方向跌落去了。看起來就好像是保齡球吸引乒乓球一樣。只要把這個比喻變成四維版本,或多或少就跟物理現實一樣。
質量扭曲時空亦會導致一個牛頓力學沒有的結論,可以用來檢驗廣義相對論是否正確。由於重力不是一種力而是時空曲率,那麼就連沒有質量的光也會「跌落」時空的凹陷裡。1919 年,天文學家愛丁頓遠征非洲觀察日全食,記錄天狗食日時太陽附近的星光。他對比其他時候所觀察到同一天區的星星,發現星星的位置有輕微偏差,數值恰好與廣義相對論的預言吻合。
星光偏折是愛因斯坦廣義相對論的首個驗證。現在,天文學家利用觀察超大質量黑洞或星系團造成的光線偏折去研究非常遙遠的星系。這個類似光學透鏡的效應,叫做重力透鏡(gravitational lensing)。除此之外,廣義相對論還預測了很多物理效應,都已被一一證實。例如水星近日點進動(mercury perihelion precession),其數值與使用廣義相對論計算一致;時空會被自轉的星球扭曲,叫做參考系拖拽(frame dragging),已被人造衛星驗證;重力場越強時間流逝速率越慢,叫做重力時間遲滯(gravitational time dilation),已被非常準確的原子鐘證實;2015 年正值愛因斯坦發表廣義相對論 100 週年,人類終於直接探測到廣義相對論的最後一個未驗證的預言——重力波(gravitational wave),這是極大質量在時空中產生的漣漪。
重力波以光速前進,就跟重力傳遞的速度一樣。太陽平均距離地球 1 億 5 千萬公里,即光太約要走 8 分 20 秒的路程。假如太陽此刻突然消失,地球仍然會繞著前太陽位置繞 8 分 20 秒左右,才會「感到」太陽的重力消失了。
愛因斯坦的錯誤
不過,愛因斯坦一開始並不相信重力波存在。他移居美國後寫了一篇論證重力波不存在的論文,投到美國一家期刊。當年,同儕審查(peer review)在美國科學界已經是常規,但在德國科學界卻不然。愛因斯坦因為不滿期刊未經他同意就將論文交給一位專家審閱,忿而徹回了該論文。後來,愛因斯坦發現他論文中用來證明重力波不存在的數學出了錯。現在看來,他徹回論文此舉令他得以發現這個錯誤。
另一個關於廣義相對論的愛因斯坦犯下的錯,就是耳熟能詳的宇宙膨脹。愛因斯坦發現,他親手推導出來的場方程式說,宇宙不是正在膨脹就是在收縮。這是因為重力的本質,時空扭曲只會令物體互相吸引,不會排斥。愛因斯坦認為宇宙必然是靜止的,因此就在方程式裡加入了一個常數項用來平衡吸引力。這個常數項就是上述愛因斯坦場方程中的
^g_uv,其中 ^ 就是所謂的宇宙常數。1929 年,哈勃發現宇宙正在膨脹,愛因斯坦就徹回了宇宙常數。現在,天文學家發現宇宙非但正在膨脹,而且膨脹正在加速,愛因斯坦加入宇宙常數似乎是正確的。
廣義相對論的展望
今天,很多物理學家在找尋比廣義相對論更上一層樓的新時空理論。雖然廣義相對論的預言從未出錯,但我們知道,它至少不是關於宇宙的完整理論,因為廣義相對論與量子力學並不相容。理論物理學家們正埋首研究量子重力理論,而天文學家們也正不斷以新的觀測去測試廣義相對論。沒有人知道再過百年之後,廣義相對論會否仍是主宰時空的理論。但愛因斯坦與相對論,肯定佔有人類文明史冊之中極重要的一頁。
摘自 https://hfdavidyu.com/2017/05/25/einstein_general_relativity/#comments



